Table of Contents
Support Vector Machine
Classification
- Classification is a fundamental task in machine learning where the goal is to assign new input data to one of several predefined categories or classes.
- It’s a form of supervised learning, meaning that the model is trained on a labeled dataset where the correct output (class) is known.
- Example Bank Loan application. This can be either accepted or rejected. Predefined attributes for this classification could be as below
- Applicant annual income
- Applicant credit history
- Applicant age
- Applicant Net worth (Assets minus liabilities)
- We will have historical data points of above attributes for various earlier applicants. Further we will also have details of the loan application outcome- Accepted or Rejected. In machine learning models like SVM (Supervised Vector Machine) will train the model on these attributes and previous outcomes. Any new application based on model training will be classified by the model as either Accepted or Rejected
- Illustrative use cases of classification tasks
- Spam Detection: Classifying emails as “spam” or “not spam.”
- Medical Diagnosis: Predicting whether a patient has a disease based on medical records
Support Vector Machine
Support Vector Machine is a Machine learning model which provides classification functionality.
It can handle both linear and Nonlinear data
- Linear Data: Straight-line relationship between input variables (features) and the output variable (target).
- Non-Linear Data: Relationship between variables is not proportional and may involve curves or more intricate patterns.
Key concepts of SVM
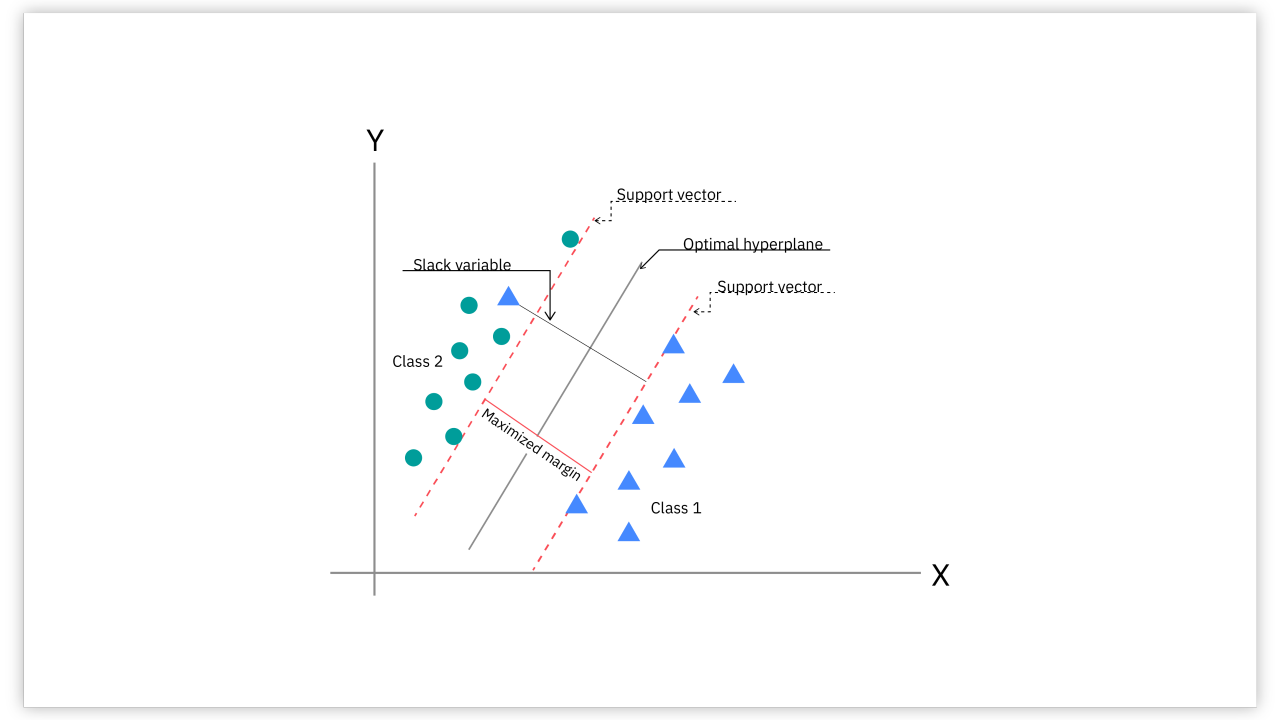
- Hyperplane: A Hyperplane is a line which divides the points in n-plane into two categories.
- Margin: The distance between the hyperplane and the nearest data points from each class. SVM aims to find the hyperplane that maximizes this margin
- Support Vectors: The data points that are closest to the hyperplane
- Kernel Trick: A method used to handle non-linearly separable data by transforming it into a higher-dimensional space where it becomes linearly separable.
Linear SVM (Linearly Separable Data)
- Applied to data that can be separated by a straight line
- SVM finds the hyperplane that best separates the classes by maximizing the margin.
Process:
- Identify the support vectors.
- Compute the optimal hyperplane.
- Classify new data points based on trained data which side of the hyperplane they fall on.
Non-Linear SVM
Applied to data that cannot be separated by a straight line:
SVM transforms the data into a higher-dimensional space where it becomes linearly separable.
Process:
- Kernel Functions: Apply kernel function trick to map the original data into a higher-dimensional space. Common kernels: Linear, Polynomial, Radial Basis Function (RBF), Sigmoid.
- In the new space, find the optimal hyperplane.
- Classify new data points by mapping them into the higher-dimensional space and applying the hyperplane.
Applying SVM to classic iris dataset for understanding
Iris Dataset: Contain measurement of flowers
- Features: Petal length, Petal width, Sepal length, Sepal width.
- Classes: Setosa, Versicolor, Virginica
Steps
Data Preparation-1
- Collect Data: Obtain measurements for each iris flower.
- Label Data: Each data point is labeled with its species.
Visualize the Data – 2
- Plot the data to see if it’s linearly separable
Choose SVM Parameters -3
- Since Setosa is linearly separable from others, we can use a Linear SVM for this binary classification (Setosa vs. Non-Setosa)
Train the SVM Model-4
- Compute Hyperplane: The SVM algorithm calculates the hyperplane that maximizes the margin between the two classes
- Identify Support Vectors: These are the Setosa and Non-Setosa samples closest to Hyperplane
Make Predictions -5
- New Data Point: A new iris flower with specific measurements.
- Classification: Plug the measurements into the hyperplane equation to determine on which side of the hyperplane the point falls
Mathematical Explanation of SVM
- Select a subset of the Iris dataset for simplicity.
- Explain the SVM algorithm step by step using this subset.
- Perform calculations to find the optimal hyperplane.
Select a Subset of the Iris Dataset
The Iris dataset consists of three classes:
- Setosa
- Versicolor
- Virginica
We’ll perform binary classification between Setosa and Versicolor, using only two features:
- Feature 1: Petal Length (in cm)
- Feature 2: Petal Width (in cm)
Setosa (Class -1)
Sample | Petal Length (X1) | Petal Width (X2) | Class (Y) |
1 | 1.4 | .2 | -1 |
2 | 1.4 | .2 | -1 |
3 | 1.3 | .2 | -1 |
Versicolor (Class +1)
Sample | Petal Length (X1) | Petal Width (X2) | Class (Y) |
4 | 4.7 | 1.4 | +1 |
5 | 4.5 | 1.4 | +1 |
6 | 4.9 | 1.5 | +1 |
Note: We assign -1 to Setosa and +1 to Versicolor for mathematical convenience.
SVM Algorithm Steps
Objective: Find the hyperplane that separates the two classes by maximizing the margin between them.
Hyperplane Equation in two dimensions
- ] : Weight vector normal to the hyperplane
- b is the bias term
- : Vector or data points
Verification / Constraint for correctly classified data points
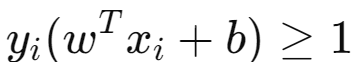
- Yi: Class label for mathematical convenience. Setosa labeled as -1. Versicolor labeled as +1
- Xi : Data points
- b: Bias factor
- Wt : Weight vector normal to the Hyperplane
Margin : SVM objective is to find Hyperplane which maximize the Margin
The margin M is
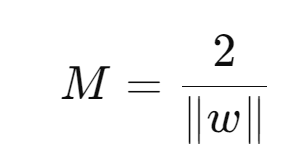
To maximize the margin, we need to minimize the value of II w II dividing 2
Perform calculations to find the optimal hyperplane
Feature and Labels
Setosa (Class -1)
Sample | Petal Length (X1) | Petal Width (X2) | Label (Y) |
1 | 1.4 | .2 | -1 |
2 | 1.4 | .2 | -1 |
3 | 1.3 | .2 | -1 |
Versicolor (Class +1)
Sample | Petal Length (X1) | Petal Width (X2) | Label (Y) |
4 | 4.7 | 1.4 | +1 |
5 | 4.5 | 1.4 | +1 |
6 | 4.9 | 1.5 | +1 |
Hyperplane Equation in two dimensions
Objective to find W1, W2, b with below constraints:
- The margin is maximized (i.e., ∥w∥ which divide 2 is minimized).
- The constraints
 are satisfied. Here Yi is class label (-1, +1), Xi are data points, b is the bias factor and Wt is the weight vector normal to the Hyperplane
are satisfied. Here Yi is class label (-1, +1), Xi are data points, b is the bias factor and Wt is the weight vector normal to the Hyperplane
Hyper Plane Equation
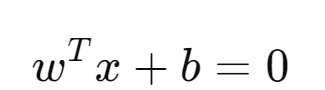
X are the data points
W is weight assigned to data point
B is the bias factor
Support Vector Points equation (Data points which lie on Margin)
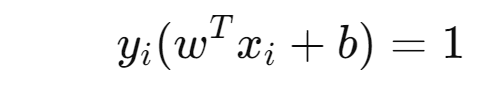
Equation / Constraint for any other datapoints (other than Support vector points)
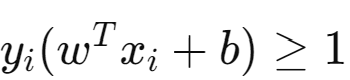
Identifying Support Vectors
The support vectors are the data points closest to the hyperplane. For our dataset, these are:
- Setosa (Class -1): Point 3 (1.3, 0.2)
- Versicolor (Class +1): Point 4 (4.7, 1.4)
Point 3 (i=3i)
−1(w1×1.3+w2×0.2+b) =1
−(1.3w1+0.2w2+b) =1
⇒1.3w1+0.2w2+b= − 1 # Equation 1
Point 4 (i=4)
+1(w1×4.7+w2×1.4+b) =1
4.7w1+1.4w2+b= 1 # Equation 2
As there are three variable in above two equations x,y,b let’s subtract Equation 1 from 2 to have an equation with two variable
Equation 3
Calculate W1
Assume W2 =1 to solve the above equation
.8/3.4
= W1 = 0.2353
Calculate b by substituting w1, w2 in Equation 1 above
The hyperplane equation in 2 dimension is
0.2353 x1 + x2 −1.5059 = 0
Calculating the Margin
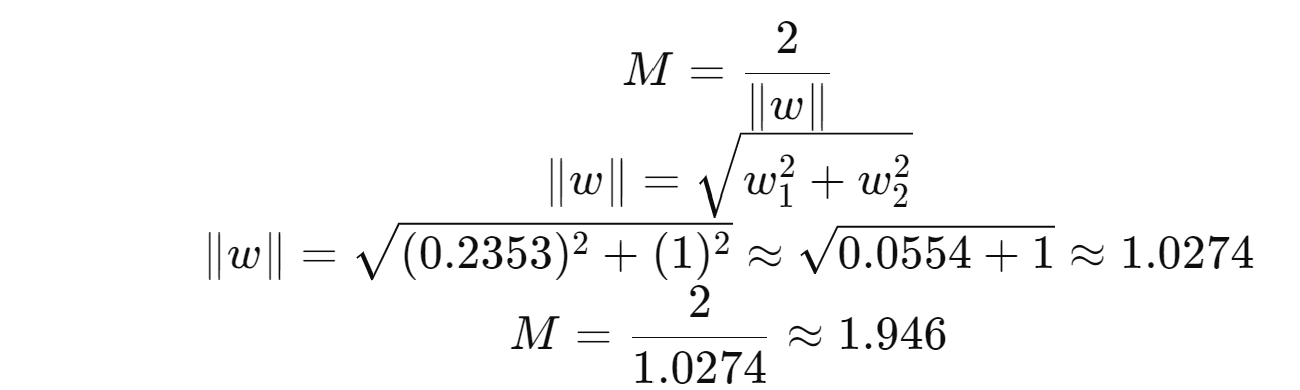
Verification of Constraints
Now verify the values of w1, w2, b by passing them to each data points constraints in below 2 dimensions equation
If any of the points does not satisfy above constraint than we have to recalculate values of w1, w2, b. This time let’s use R to find the values of W1, W2, b
Using R to find Hyperplane in SVM
The Iris dataset is a classic dataset in machine learning, containing measurements of iris flowers from three species
Steps in R
- Load the necessary libraries. e1071 package, which provides the svm () function.
- Load the iris dataset The iris dataset is available in R by default
- Train a Support Vector Machine (SVM) model. Use the svm () function to train the model.
- Make predictions using the trained SVM model
- Evaluate the model’s performance. Use a confusion matrix to evaluate the accuracy of the model.
Load the necessary libraries

Load the iris dataset

Train a Support Vector Machine (SVM) model
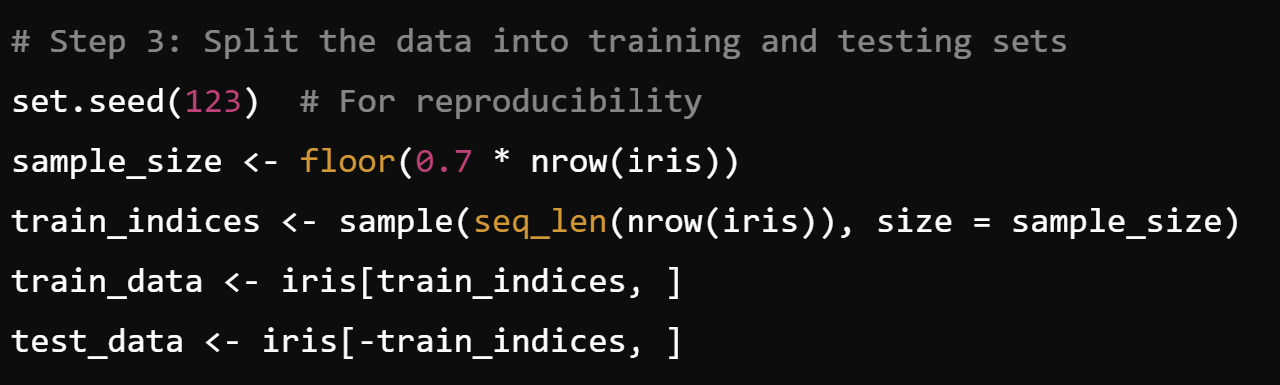
Explanation
- The set.seed() function ensures that the random operations (like sampling) produce the same result each time you run the code.
- nrow(iris): This returns the number of rows in the iris dataset, which is 150 because the dataset has 150 samples.
- 0.7 * nrow(iris): Here, we’re calculating 70% of the total number of rows in the iris dataset, which is 0.7×150=1050.7 \times 150 = 1050.7×150=105. This means we want 105 samples for training.
- floor(): The floor() function rounds down the result to the nearest whole number.
- seq_len(nrow(iris)): This generates a sequence of numbers from 1 to the number of rows in the dataset, i.e., from 1 to 150.
- sample(seq_len(nrow(iris)), size = sample_size): The sample() function randomly selects 105 row indices (because sample_size is 105) from the sequence 1:150. These row indices represent the samples that will go into the training set.
- iris[train_indices, ]: This selects the rows of the iris dataset corresponding to the indices in train_indices. These 105 samples will be used for training the model.
- iris[-train_indices, ]: The -train_indices part means “exclude the rows that are in train_indices.” This creates the test set with the remaining 45 samples (150 – 105 = 45), which will be used for evaluating the model.

Explanation
- svm_model <-: This is an assignment operation. The result of the svm() function will be stored in the object called svm_model.
- svm():This function is used to train a Support Vector Machine model. It belongs to the e1071 package
- Species ~ .: Species: This is the target variable, i.e., the variable that we want to predict. It has three possible values: setosa, versicolor, and virginica.
- . (dot): This is a shorthand for including all the other columns of the dataset as independent (input) variables. In this case, the independent variables are the features of the iris flower: Sepal.Length, Sepal.Width, Petal.Length, and Petal.Width.
- The formula Species ~ . tells the SVM model to predict Species based on the other columns in the dataset.
- kernel = “linear”: A kernel function in SVM is used to transform the data into a higher-dimensional space to find the optimal hyperplane that separates the classes. Other kernel : radial: Radial Basis Function (RBF) kernel, used for non-linear classification problems. polynomial: A polynomial kernel, used when the relationship between classes is more complex. sigmoid: Sigmoid kernel, similar to the activation function in neural networks.

Prediction: The predict() function is used to predict the class labels on the test data.

Explanation
- predict(): This function takes the trained svm_model and applies it to the test_data to predict the species of the flowers.
- table(): This function is used to create a confusion matrix, which is a summary table that shows how well the model performed in classifying the test data.
- Predicted = predictions: This is the predicted species for each test sample as generated by the model.
- Actual = test_data$Species: This is the actual (true) species of each flower in the test_data.
- This confusion matrix compares the predicted species (rows) with the actual species (columns).

Accuracy: The accuracy is calculated by dividing the correctly classified samples by the total number of samples.
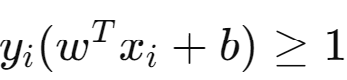 are satisfied. Here Yi is class label (-1, +1), Xi are data points, b is the bias factor and Wt is the weight vector normal to the Hyperplane
are satisfied. Here Yi is class label (-1, +1), Xi are data points, b is the bias factor and Wt is the weight vector normal to the Hyperplane