Model Validation

Model Validation

• Model validation is the process of evaluating a machine learning model’s performance on data it hasn’t seen during training. The goal is to ensure that the model generalizes well to new, unseen data

Data Splitting

Data set typically split into three sets

• Training Set
• Validation Set
• Test Set

Training Set

• Definition: The portion of the dataset used to train the model.
• Typical Size: Usually the largest portion (e.g., 60-80% of the total data).

Validation Set

Definition: A subset of data used to evaluate the model during training.

Typical Size: Around 10-20% of the data

Test Set

Definition: A separate subset used to provide an unbiased evaluation of a final model fit.

Typical Size: Around 10-20% of the data.

Real Effect (True Effect)

• A real effect refers to the actual, meaningful relationship between variables in a dataset. It represents the underlying pattern or structure in the data that is not due to chance or randomness. A model that captures the real effect successfully identifies these patterns
• Example: Imagine you’re building a model to predict house prices based on features like the number of bedrooms, location, and square footage. If the model consistently identifies that houses with more square footage and better locations tend to be more expensive, that’s likely a real effect

Random Effect (Noise)

• A random effect (also called noise) refers to patterns in the data that appear due to chance, randomness, or idiosyncrasies of the dataset but do not represent any true relationship. A model that captures random effects is overfitting
• Example: Continuing with the house price example, suppose the model finds that houses listed with the word “beautiful” in their descriptions tend to have higher prices. This might be a random effect

K-Fold Cross-Validation

K-Fold Cross Validation

• K-Fold Cross-Validation is a specific type of cross-validation where the dataset is divided into K equal (or nearly equal) parts called folds.
• The model is trained and validated K times, each time using a different fold as the validation set and the remaining K-1 folds as the training set.
• The final performance metric is then computed as the average of the metrics across all K trials.

Explanation with an Example

We have a small dataset of 100 observations for a regression problem, and we want to evaluate a machine learning model (e.g., Linear Regression) using 5-Fold Cross-Validation.

Step 1: Prepare the Dataset

• Total Data Points: 100 observations
• Features (X): Predictor variables
• Target (Y): Response variable

Step 2: Choose the Value of K

• K = 5
• This means we’ll split the dataset into 5 folds.

Step 3: Split the Dataset into K Folds

• Fold 1: Observations 1-20
• Fold 2: Observations 21-40
• Fold 3: Observations 41-60
• Fold 4: Observations 61-80
• Fold 5: Observations 81-100

Step 4: Perform K Iterations (Training and Validation)

• For each iteration i from 1 to K:
• Validation Set: Use the i-th fold as the validation set.
• Training Set: Use the remaining K-1 folds as the training set.
• Train the Model: Fit the model on the training set.
• Evaluate the Model: Assess the model’s performance on the validation set.
• Record the Performance Metric: Store the metric (e.g., Mean Squared Error).

Steps in Detail

Iteration 1 (Fold 1 as Validation Set)

• Training Set: Folds 2, 3, 4, 5 (Observations 21-100). Train the Model on observations 21-100.
• Predict on observations 1-20. (Fold 1 as Validation Set)
• Calculate Performance Metric (e.g., Mean Squared Error, MSE). Suppose MSE1 = 10.5

Iteration 2 (Fold 2 as Validation Set)

• Training Set: Folds 1, 3, 4, 5 (Observations 1-20 and 41-100). Train the Model on observations 1-20 and 41-100.
• Predict on observations 21-40. (Fold 2 as Validation Set)
• Calculate Performance Metric (e.g., Mean Squared Error, MSE). Suppose MSE2 = 9.8

Iteration 3 (Fold 3 as Validation Set)

• Training Set: Folds 1, 2, 4, 5 (Observations 1-40 and 61-100). Train the Model on observations 1-40 and 61-100.
• Predict on observations 41-60. (Fold 3 as Validation Set)
• Calculate Performance Metric (e.g., Mean Squared Error, MSE). Suppose MSE3 = 11.2

Compute the Average Performance Metric

Average MSE = (MS1 +MSE2+MSE3 + MSE4 +MSE5)/5 =

• MSE = (10.5 + 9.8 + 11.2 + 10 +9.5) /5 = 10.2

Interpret the Results

• Model Performance: The model has an average Mean Squared Error of 10.2 across all folds.

Standard Deviation of MSE

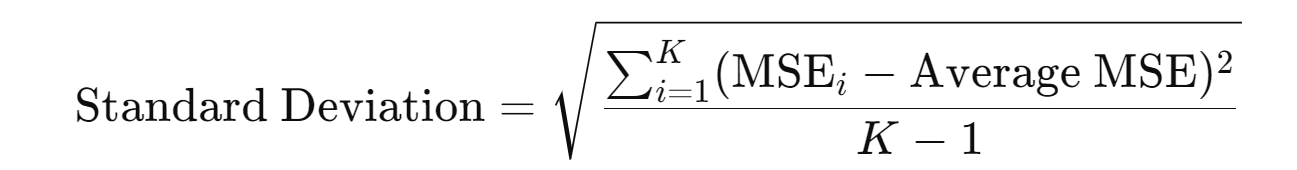
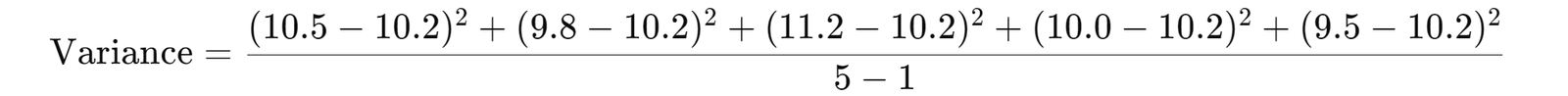
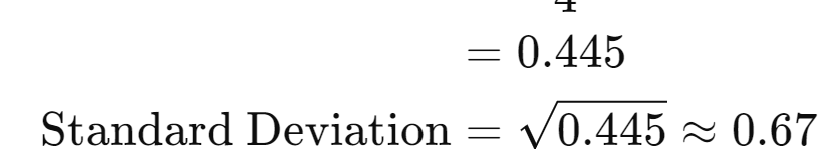
• Interpretation: The standard deviation is 0.67, indicating moderate variability in model performance across folds.
  1. 1. 
        Benefits of K-Fold Cross-Validation
• All data points are used for both training and validation.
• Reduced Overfitting: By training and validating on different subsets, the model’s ability to generalize is tested.
• K = 5 or K = 10: Provides a good balance between bias and variance.

Summary:

• K-Fold Cross-Validation is a technique used to assess the performance of a model by splitting the dataset into K subsets, training the model on K-1subsets, and testing on the remaining subset, repeating this process 𝐾 times.
• The final performance metric is the average of the results from each iteration.
• It reduces the bias and variance in performance estimation, making it a reliable method for evaluating machine learning models, especially when data is limited.